Elasticity, as it is used in economics, refers to the response of a "dependent" variable to changes in the "independent" variable. A good way to remember this is that the "dependent" variable depends upon the "independent" variable. One can construct an elasticity for any two variables that are related. For instance: a price elasticity tells us how changes in price affect the quantity demanded; an income elasticity tells us how changes in income affect the quantity demanded; and a cross-price elasticity tells us how the quantity demanded for good X is affected by changes in the price of good Y. The cross price elasticity can be used to determine whether a related good - in this case good Y - is a "substitute good" or a "compliment good." The methodology used to develop a price elasticity is the same method used to construct an income or cross-price elasticity.

This handout develops a demand elasticity (noted E_D) where the quantity demanded depends upon the price:

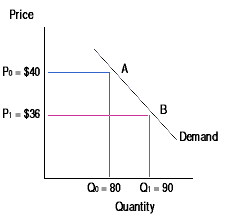
Above we have two points on a demand curve, each has a unique price and quantity. Lets first look at a price decrease from point A to point B. The question of interest is this: What is the percentage change in quantity demanded associated with the percentage change in price?

In mathematical terms:

Elasticity of Demand = (% change in quantity) / (% change in price)

where: P is referred to as the base price and Q is referred to as the base quantity

Given the above example, if we begin at point A and look at a price decrease to point B, our original price (P₀) is $40 and our original quantity (Q₀) is 80. We would be choosing P₀ and Q₀ as the respective bases. We could just as well use P₁ and Q₁ as the respective bases. But - the base you choose affects the value of the calculated elasticity. Neither way is exclusively the "correct" way. These are referred to as POINT ELASTICITIES because either point A or point B is chosen as the base.

One way around the choice of base problem is to calculate what we call the ARC ELASTICITY OF DEMAND. With ARC ELASTICITY OF DEMAND, rather than picking P₀ or P₁ as the base, we can use the average of P₀ and P₁ as the base. The ARC ELASTICITY OF DEMAND value will always fall between the point elasticities.

We will use the ARC ELASTICITY OF DEMAND exclusively. It simply uses a different base. Instead of picking the P₀ and Q₀ as base or the P₁ and Q₁ as base we use Parc and Qarc.

where:

Parc = (P₀ + P₁) / 2 and Qarc = (Q₀ + Q₁) / 2

This means that the ARC ELASTICITY OF DEMAND is equal to:

where:

Using the values in the above example do the following:

1.) Calculate the point elasticity of demand using P₀ and Q₀ as the base.
2.) Calculate the point elasticity of demand using P₁ and Q₁ as the base.
3.) Calculate the ARC elasticity of demand.

I have had you calculate the point elasticities to convince you that the arc elasticity falls between them. FROM NOW ON, WHEN ASKED TO CALCULATE THE DEMAND ELASTICITY, CALCULATE THE ARC ELASTICITY OF DEMAND.

Calculate only the ARC elasticity for the following. In each case state whether the calculated value is elastic, inelastic, or unitary. Explain what these three words mean in your own words.
4.) P₀ = $89; Q₀ = 1000; P₁ = $99; Q₁ = 950
5.) P₀ = $89; Q₀ = 1000; P₁ = $99; Q₁ = 700
6.) P₀ = $69; Q₀ = 200; P₁ = $79; Q₁ = 195
7.) P₀ = $3.99; Q₀ = 12,000; P₁ = $3.79; Q₁ = 12,950

What are the major determinants of price elasticity?

1) Substitutability: The most important determinant is the number and degree of similar products that exist. More and better available substitutes make the elasticity increase. Consumers become quite price sensitive when there are a host of available substitutes.

2) Budget Share: If the product is a very small percentage of the budget then the consumer may be very insensitive to price. For instance, if I purchase toothpicks on a box of 200 for $1.49 and the price goes to $2.99 for some reason I will likely continue to buy the toothpicks. A good way to remember this is "the importance of being unimportant."